Finished Report: PDF
Finished Presentation: PDF
*****IN PROGRESS*****
Normal form of the bifurcation
It is an iterative map $F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ such that
\[\boldsymbol{x}_{n+1}= F(\boldsymbol{x_n})=\begin{cases}A_{L} \boldsymbol{x}+\boldsymbol{m} & x \leqslant 0 \\ A_{R} \boldsymbol{x_n}+\boldsymbol{m} & x \geqslant 0\end{cases}\]where
\(A_{\alpha}=\left[\begin{array}{cc}T_{\alpha} & 1 \\ -D_{\alpha} & 0\end{array}\right],\quad (\alpha=L \text{ or } R)\) $L$ and $R$ indicate Left or Right side of the y-axis.
\[\boldsymbol{m}=\left[\begin{array}{l}\mu \\ 0\end{array}\right],(\mu \text{ is a constant}) \quad \boldsymbol{x_k}=\left[\begin{array}{l}x_{k}\\y_{k}\end{array}\right]\]In matrix notation:
\[\left[\begin{array}{l}x_{n+1} \\ y_{n+1}\end{array}\right]=\left[\begin{array}{cc}T_{\alpha} & 1 \\ -D_{\alpha} & 0\end{array}\right]\left[\begin{array}{l}x_{n} \\ y_{n}\end{array}\right]+\left[\begin{array}{l}\mu \\ 0\end{array}\right]\]Some preliminary random test with the map $F$
Four parameters $T_{L}, D_{L}, T_{R}, D_{R}$ are randomly chosen from the interval $(-2,2)$.
Let $\mu=1$ without loss of generality.
Start the iteration $F$ from origin \(\left[\begin{array}{l}0 \\ 0\end{array}\right]\)
Number of iterations $n=2000$ or $n=500$
Following pictures are observed.
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
Some uninteresting pictures where a straight line appears are omitted. For example,
.png)
Restrictions on $A_R$
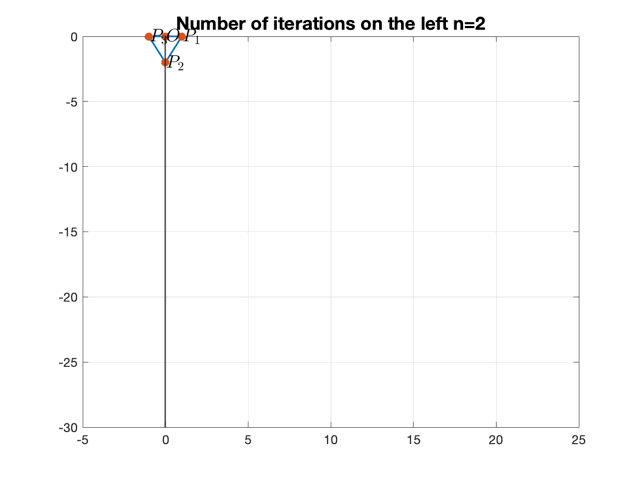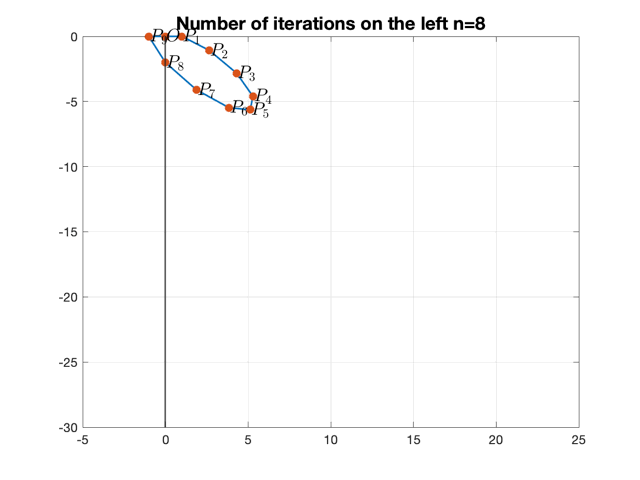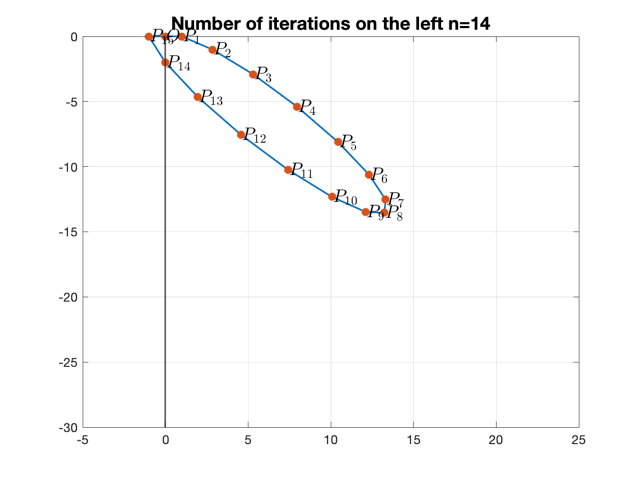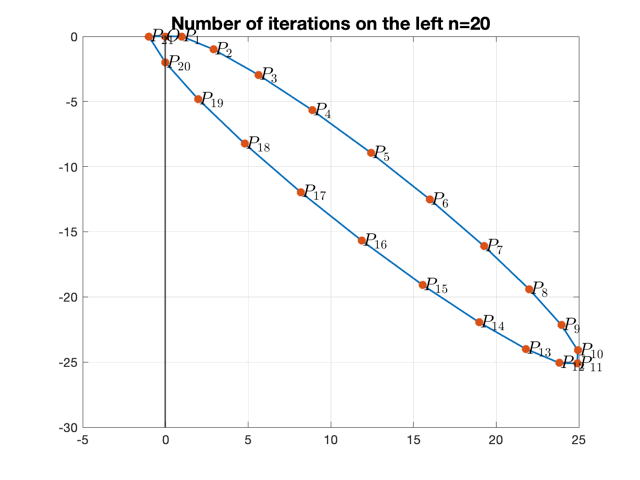
Now if we put restriction on $A_R$, i.e. $T_{R}, D_{R}$, such that under $n$ iterations on the right, the point lands on y-axis:
\[F^n(O)=\left[\begin{array}{l}0 \\ y_n\end{array}\right]\]It is no doubt that \(\left[\begin{array}{l}0 \\ y_n\end{array}\right]\) will then be mapped to some point on the x-axis: \(\left[\begin{array}{}y_n+\mu \\ 0\end{array}\right]\)
Let $y_n=-2$ in our case.
Still let $\mu=1$.
Following ploygons are generated for different $n$.
.png)
.png)
.png)
.png)
For a series of $n$, under the same scale in axes, it is easy to see the behaviour of the ploygons for increasing $n$ with a GIF image: